Diffusion Models for Speech Enhancement
Introduction
In the past decade, speech enhancement algorithms have benefited greatly from the introduction of data-driven approaches based on deep neural networks (DNNs) . Among them, a broad class of methods utilizes predictive models that learn to map a given input to a desired output. In a typical supervised setting, a predictive model is trained on a labeled dataset to minimize a certain point-wise loss function between the processed input and the clean target. Following the principle of empirical risk minimization, the goal of predictive modelling is to find a model with minimal average error over the training data, where the generalization ability of the model is usually assessed on a validation set of unseen data. By employing ever-larger models and datasets—a current trend in deep learning—strong generalization can be achieved. However, many pure data-driven approaches are considered black boxes and remain largely unexplainable and non-interpretable. Moreover, these models typically produce deterministic outputs, disregarding the inherent uncertainty in their resultsGenerative models follow a different learning paradigm, namely estimating and sampling from an unknown data distribution. This can be used to infer a measure of uncertainty for their predictions and to allow the generation of multiple valid estimates instead of a single best estimate as in predictive approaches. Furthermore, incorporating prior knowledge into generative models can guide the learning process and enforce desired properties about the learned distribution. In particular, diffusion models emerged as a distinct class of deep generative models that boast an impressive ability to learn complex data distributions such as that of natural images, music, and speech. Diffusion models generate data samples through iterative transformations, transitioning from e.g. a Gaussian prior distribution to a target data distribution, as visualized in Figure 1. This iterative generation scheme is formalized as a stochastic process and is parameterized with a DNN trained to address a Gaussian denoising task.
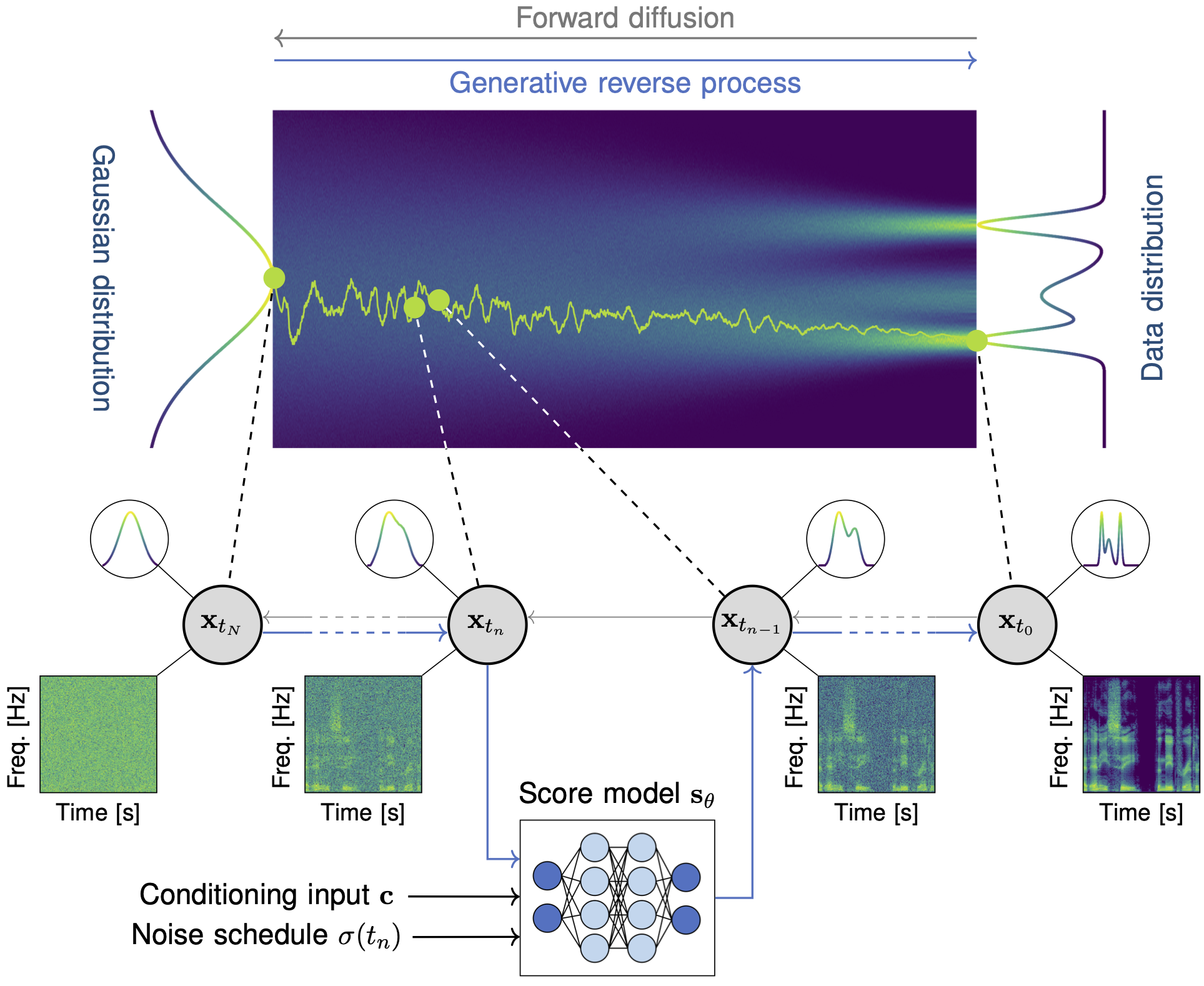
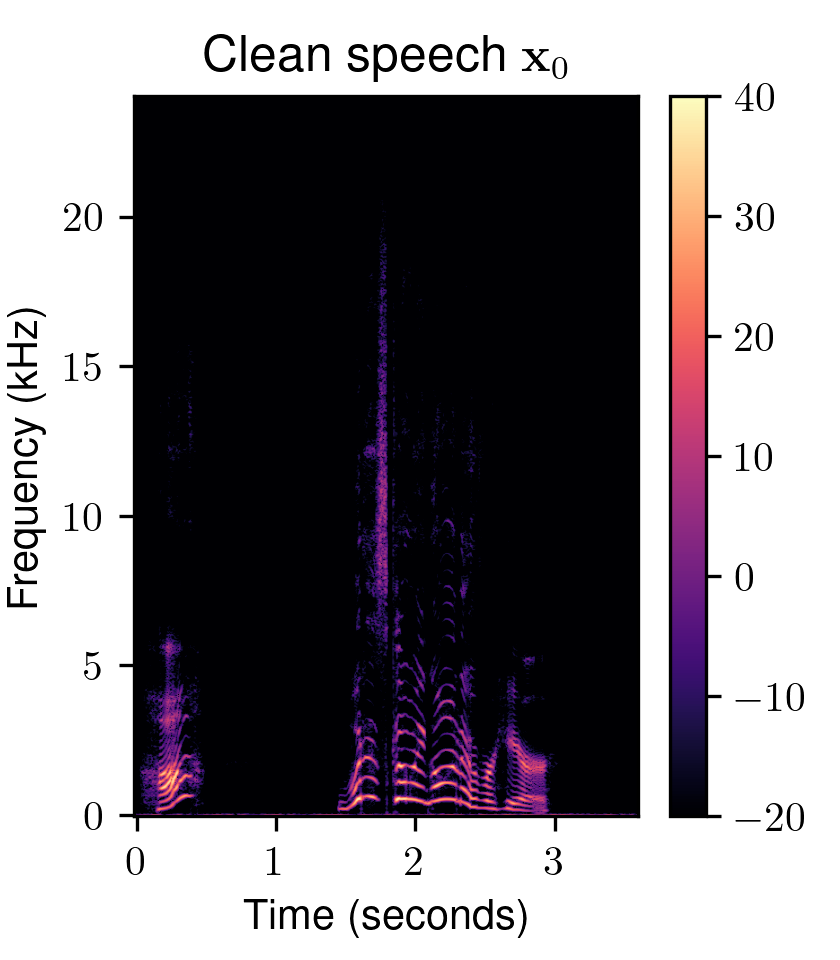
Figure 1: A continuous-time diffusion model transforms (left) a Gaussian distribution to (right) an intractable data distribution through a stochastic process \({\mathbf{{x}}_{{{t}}} \in [0, T]}\) with marginal distributions \({\{ p_t(\mathbf{{x}}_t) \}_{t \in [0, T]}}\). During training, the forward diffusion is simulated by adding Gaussian noise to the data and a score model \({\mathbf{s}_\theta}\) learns the score function \({\nabla_{\mathbf{x_t}} \log p_{t}(\mathbf x_t)}\). During the generative reverse process, the process time \({t}\) is discretized to steps \({\{ t_0, \dots, t_N \}}\) and followed in reverse from \({t_N = T}\) to \({t_0 = 0}\). (Bottom) The next state \({\mathbf{{x}}_{t_{n-1}}}\) is obtained based on the previous state \({\mathbf{{x}}_{t_{n}}}\) using an estimate given by the score model. The score model is conditioned by the noise scale at the current time step, \({\sigma(t_{n})}\), and optional conditioning \({\mathbf c}\) to guide the generation such as e.g. a text description.
Conditional Generation
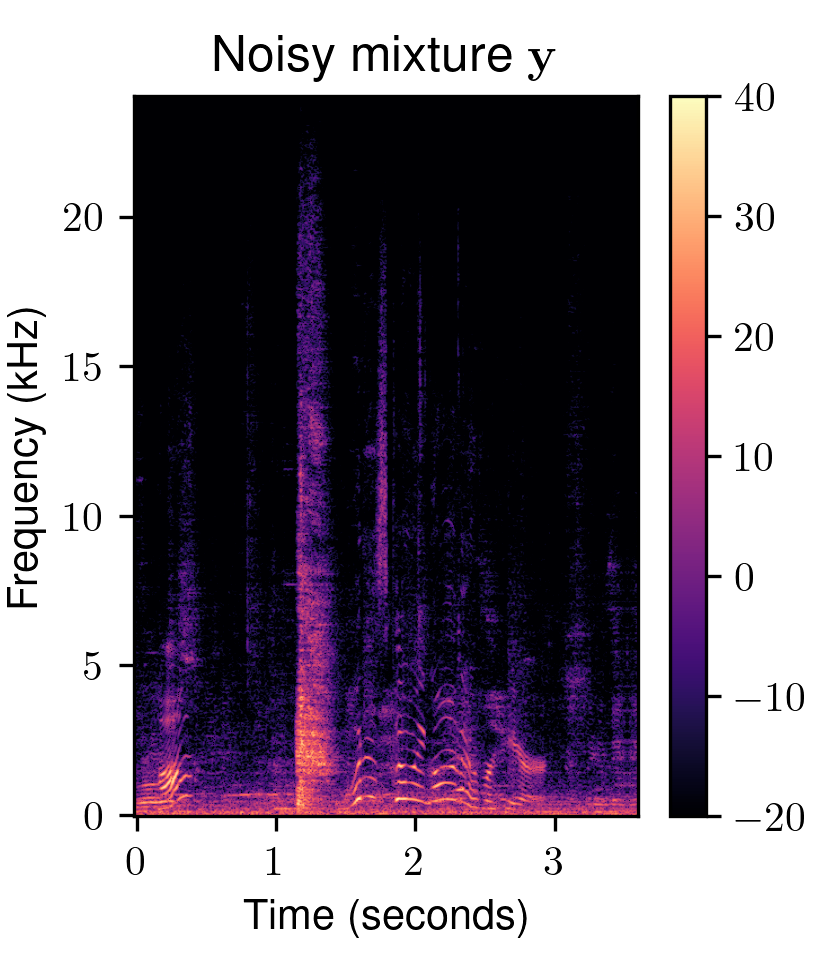
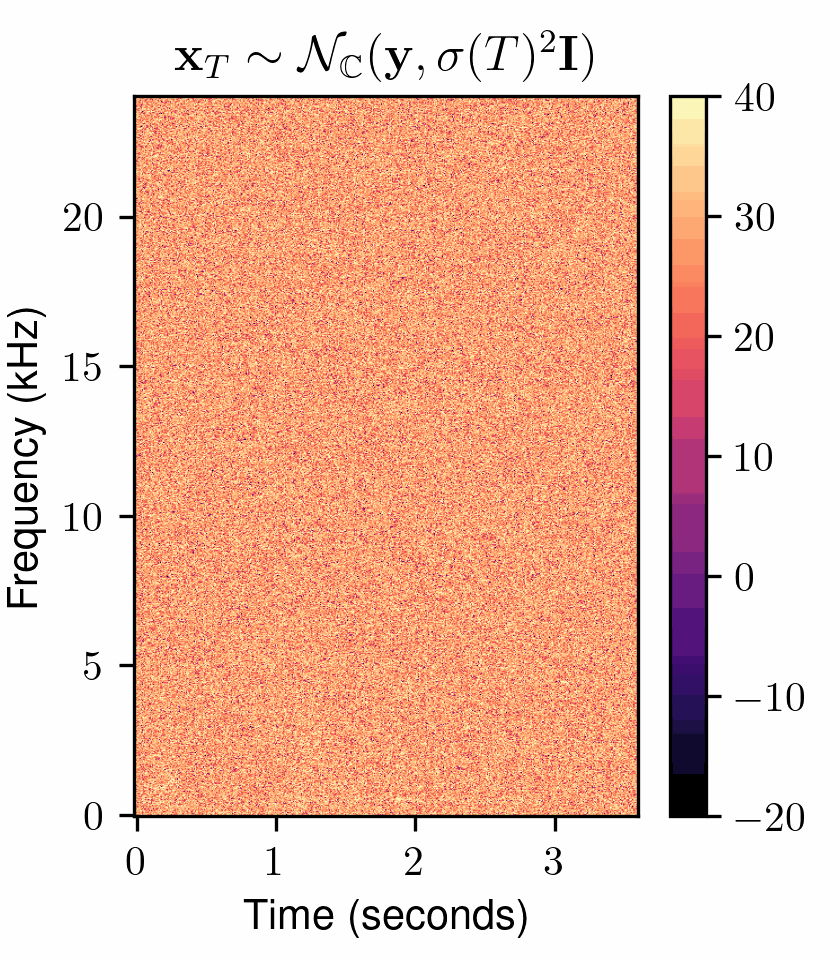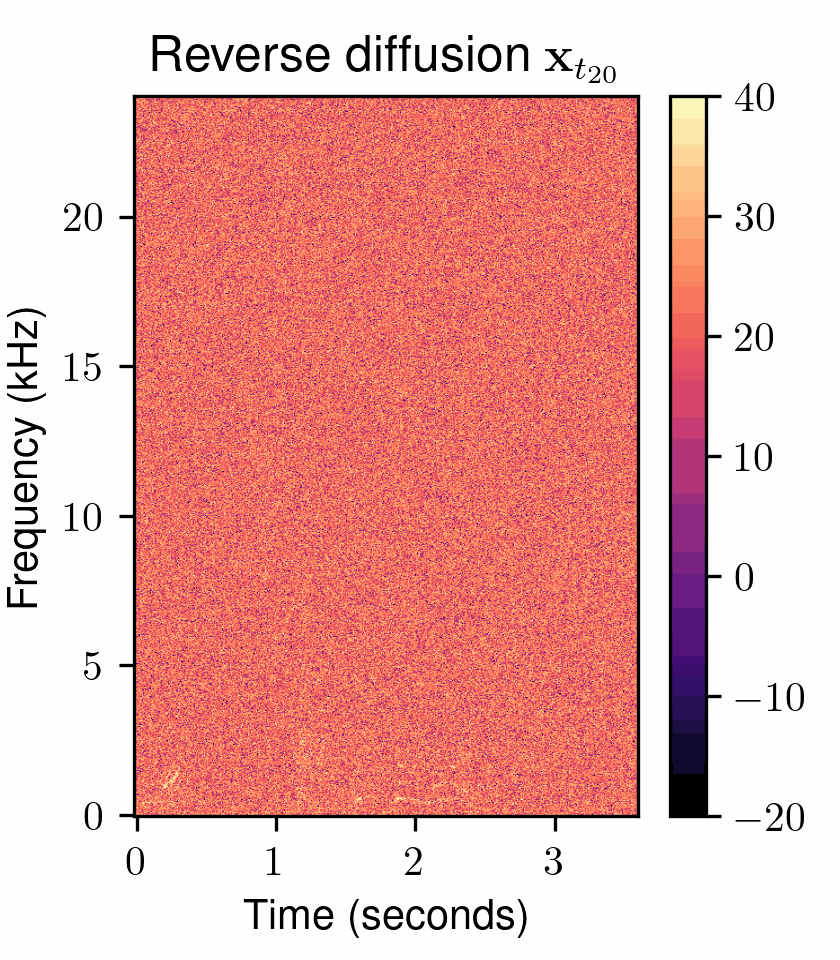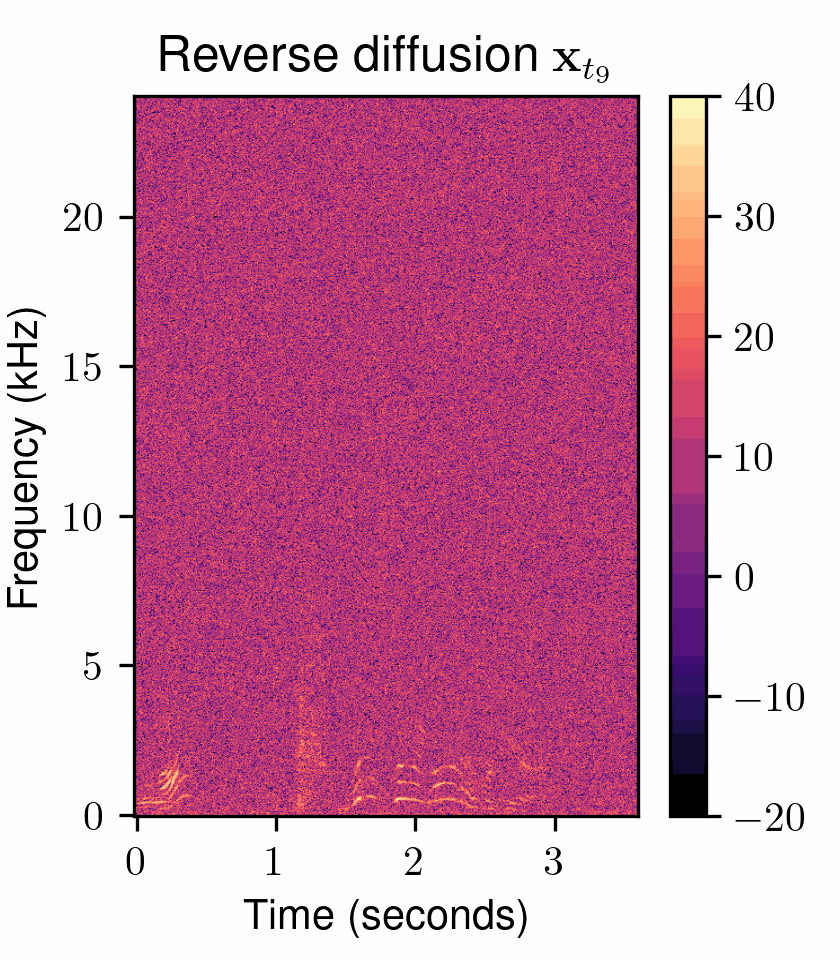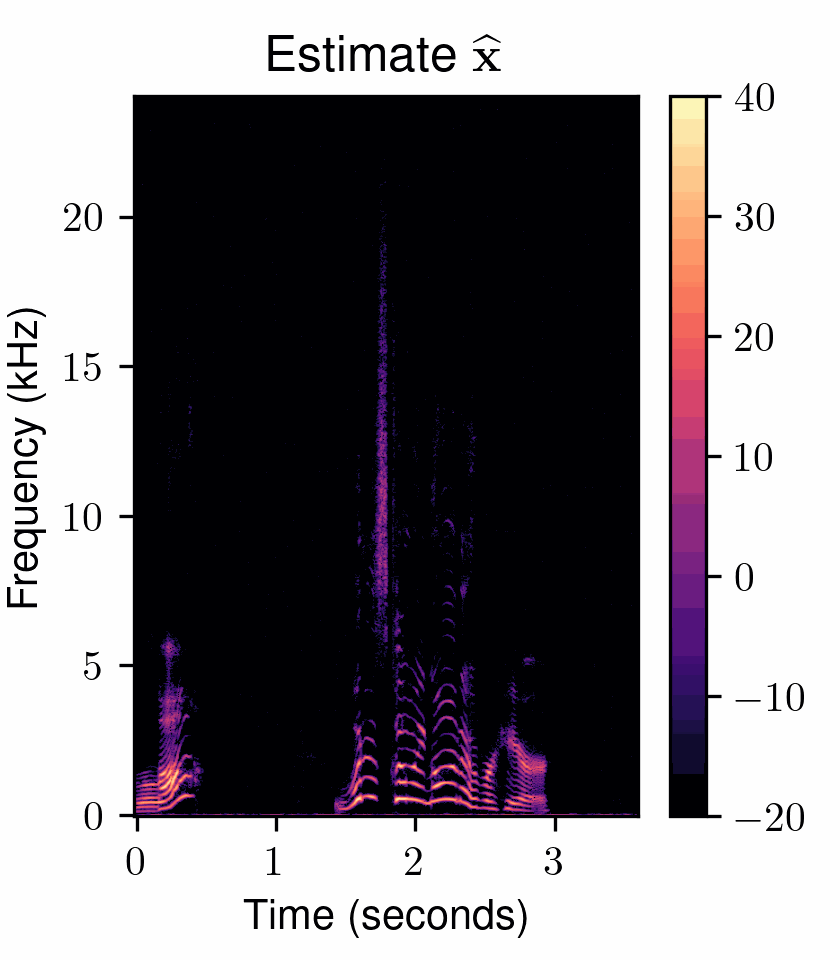
One of the most fundamental uses of diffusion models is to perform unsupervised learning from a finite collection of samples to learn an underlying complex data distribution. This provides the ability of unconditional generation, i.e., to generate new samples from the learned data distribution. To solve audio restoration tasks, a diffusion model must be adapted to generate audio that not only conforms to the learned clean audio distribution but, importantly, is also a plausible reconstruction of a given corrupted signal, which can be interpreted as a specific type of conditional generation.To this end, we use task-adapted diffusion which is based on the observation that---in many restoration tasks such as denoising, dereverberation, and separation---the corrupted signal \({\mathbf{y}}\) and the clean signal \({\mathbf{x}_0}\) belong to a common continuous space. One can thus define an adapted forward diffusion process whose mean interpolates between \({\mathbf{x}_0}\) and \({\mathbf{y}}\), as shown in Figure 2, where one classical diffusion process and two such task-adapted processes are depicted.
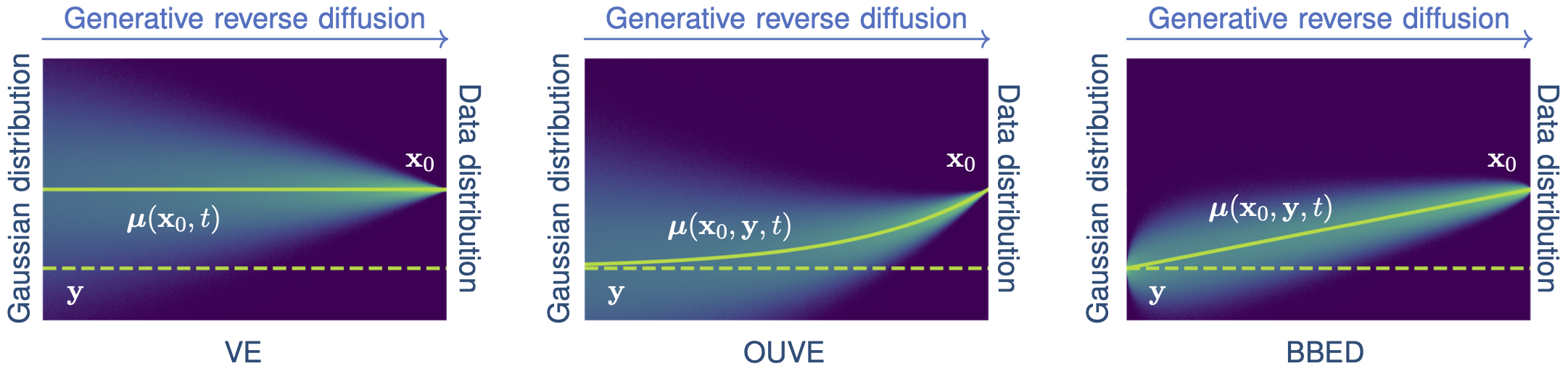
Figure 2: Comparison of different diffusion processes. (left) Variance-exploding diffusion (VE): mean is clean audio \({\mathbf x_{0}}\), independently of the degraded audio \({y}\) . (middle) Task-adapted SDE (OUVE): mean exponentially interpolates between clean audio \({x_{0}}\) and degraded audio \({y}\) . (right) Task-adapted SDE (BBED): mean linearly interpolates between clean audio \({x_{0}}\) and degraded audio \({y}\) .
 |
 |
 |
