Traditional Speech Enhancement

Introduction

Speech is one of the most natural forms of communication for human beings and poses an effective tool to exchange ideas or to express needs and emotions. Due to technical advances, speech communication is no longer restricted to face-to-face conversations but is also performed over long distances, e.g., in the form of telecommunications, or is even used as a natural way for human-machine interaction. As computationally powerful computer hardware has become available to many users, the number of speech processing devices such as smart phones, tablets and notebooks has increased. As a consequence, speech plays an important role in many applications, e.g., hands-free telephony, digital hearing aids, speech-based computer interfaces, or home entertainment systems.

With the increasing usage of mobile devices, also the demand for processing algorithms is constantly increasing. In many speech processing applications, one or more microphones are used to capture the voice of the targeted speaker. As the microphones are often placed at a considerable distance from the target speaker, e.g., in hearing aids or hands-free telephony, the received signal does not only contain the sound of the target speaker, but possibly also sounds of other speakers or background noises. Understanding speech becomes increasingly difficult, if additional sounds interfere with the desired speech sound, especially with increasing level of the interferers. Also moderate amounts of background noise that may not effect the intelligibility can reduce the perceived quality of speech.

To improve the quality and, if possible, also the intelligibility of a noisy speech signal, speech enhancement algorithms are employed. Speech enhancement can be separated in spatial filtering and spectral filtering. In spatial filtering, interfering sounds are reduced based on their spatial properties, while signals from a target direction are maintained. Spectral filtering algorithms, also known as single-channel speech enhancement, process noisy speech signals captured by a single microphone or the output of a beamformer or spatial filtering algorithm. Many approaches to enhance single-channel signals are based on the short-time Fourier transform (STFT). In the following sections, we give an overview over this approach and our contributions.

Speech Enhancement in the Fourier domain

In this section, a general STFT-based speech enhancement procedure is presented, which is shared among many single-channel enhancement algorithms. If speech is recorded in a noisy acoustic environment, e.g., as shown in Figure 1, the employed microphone does not only capture the clean speech time-domain signal \({{s}_{t}}\) but also the background noise signal \({{n}_{t}}\). Here, \({t}\) is the sample index. Under some mild constraints, the interaction of sound waves is physically well described by their superposition as shown in Figure 1.

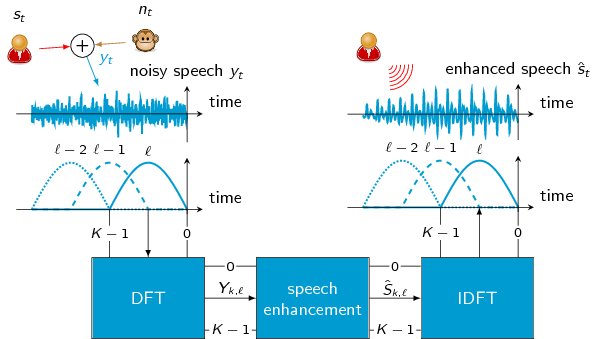
Figure 1: Block diagram of a speech enhancement algorithm operating in the STFT domain

As speech is known to be non-stationary, i.e., the speech sounds change considerably over time, the noisy input signal is split into short overlapping time segments. Each segment of the input signal is transformed to the frequency domain using the discrete Fourier transform (DFT) which results in the STFT. The aim of speech enhancement algorithms is to find an estimate of the clean speech coefficients \({\hat{{S}}_{{{k}, {\ell}}}}\) from the noisy observations \({{Y}_{{{k}, {\ell}}}}\) in the spectral domain. Here, \({k}\) is the frequency index and \({\ell}\) is the segment index. Most spectral clean speech estimators can be written in the form \[ {\hat{{S}}_{{{k}, {\ell}}}}= {{G}_{{{k}, {\ell}}}}{{Y}_{{{k}, {\ell}}}}, \] where \({{G}_{{{k}, {\ell}}}}\) is the so-called gain function. Often, the gain function is real-valued as many statistical models of the clean speech coefficients do not provide prior knowledge about the phase. Further, many algorithms estimate only the magnitude \({{A}_{{{k}, {\ell}}}}= |{{S}_{{{k}, {\ell}}}}|\) of the clean speech signal. In these cases, the enhanced speech magnitude \({\hat{{A}}_{{{k}, {\ell}}}}\) is often combined with the phase of the noisy observation \({{\Phi}^{y}_{{{k}, {\ell}}}}\) as \[ {\hat{{S}}_{{{k}, {\ell}}}}= {\hat{{A}}_{{{k}, {\ell}}}}\exp(j {{\Phi}^{y}_{{{k}, {\ell}}}}). \] We discuss approaches that exploit or modify the phase here. After estimating the clean speech spectrum \({\hat{{S}}_{{{k}, {\ell}}}}\), the time-domain signal is resynthesized using the inverse STFT. This step is also often referred to as overlap-add.

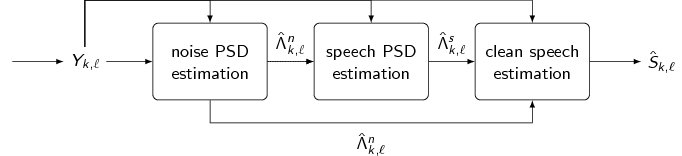
Figure 2: Block diagram of the spectral enhancement procedure

Figure 2 shows the general layout of the spectral speech enhancement step. Most clean speech estimators are derived in a statistical framework and require an estimate of the clean speech power spectral density (PSD) \({\hat{\Lambda}^{s}_{{{k}, {\ell}}}}\) and the noise PSD \({\hat{\Lambda}^{n}_{{{k}, {\ell}}}}\). Both quantities are commonly estimated blindly from the noisy observation \({{Y}_{{{k}, {\ell}}}}\). First, the noise PSD \({\hat{\Lambda}^{n}_{{{k}, {\ell}}}}\) is estimated which is used to estimate the speech PSD \({\hat{\Lambda}^{s}_{{{k}, {\ell}}}}\). Both PSD estimates are used to determine the gain function which is used to estimate the clean speech coefficients.

For the estimation of the speech and noise PSDs, non-machine-learning methods can be employed. Based on the assumption, that the background noise changes more slowly than speech, carefully designed algorithms have been proposed for this application. However, also machine-learning approaches can be used to obtain these quantities, where the properties of speech and noise are learned from representative data before the enhancement step.

Our research concerns all parts of the block diagram in Figure 2. Our solutions are based on statistical models and Bayesian theory or employ neural network based machine-learning methods.

Current Research on Speech Enhancement Using Machine-Learning and Artifical Intelligence

In our recent research, we focus on combining machine learning and statistical signal processing to obtain an improved robustness in unseen noise situations both for predictive/discriminative machine learning approaches, but also for generative approaches such as the Variational Autoencoder or Diffusion Models.

When multiple micophones are available an exciting research question is Machine Learning, Artificial Intelligence and Deep Neural Networks can be employed to obtain Nonlinear Spatial Filtering, i.e. a nonlinear joint spatial-spectral filter instead of the traditional concatenation of a linear spatial beamformer and a (nonlinear) postprocessor.

Conventional Noise PSD Estimation [1], [2]

In [1], [2], a noise PSD estimator has been presented which allows to track moderately non-stationary noise types. This algorithm describes the noisy input spectrum \({{Y}_{{{k}, {\ell}}}}\) under two different conditions: Speech presence and speech absence. Given the hypothesis \({{\mathcal{H}}_1}\), i.e., speech is present, the observed signal is modeled as \({{Y}_{{{k}, {\ell}}}}= {{S}_{{{k}, {\ell}}}}+ {{N}_{{{k}, {\ell}}}}\). Under \({{\mathcal{H}}_0}\), i.e., speech is absent, the observed signal comprises only noise as \({{Y}_{{{k}, {\ell}}}}= {{N}_{{{k}, {\ell}}}}\). The speech coefficients \({{S}_{{{k}, {\ell}}}}\) and the noise coefficients \({{N}_{{{k}, {\ell}}}}\) are assumed to follow a complex circular-symmetric Gaussian distribution. Accordingly, the likelihoods under the hypotheses \({{\mathcal{H}}_0}\) and \({{\mathcal{H}}_1}\), i.e., \({f}({{Y}_{{{k}, {\ell}}}}|{{\mathcal{H}}_0})\) and \({f}({{Y}_{{{k}, {\ell}}}}|{{\mathcal{H}}_1})\), are also modeled using Gaussian distributions. The posterior probability, i.e., the SPP \({P}({{\mathcal{H}}_1}| {{Y}_{{{k}, {\ell}}}})\), can be derived using Bayes' theorem as [1], [2] \[ {P}({{\mathcal{H}}_1}|{{Y}_{{{k}, {\ell}}}}) = {\left(1 + (1 + {\xi_{{{\mathcal{H}}_1}}}) \exp\left(-\frac{|{{Y}_{{{k}, {\ell}}}}|^2}{{\hat{\Lambda}^{n}_{{k}, {\ell}- 1}}} \frac{{\xi_{{{\mathcal{H}}_1}}}}{{\xi_{{{\mathcal{H}}_1}}}+ 1} \right)\right)}^{-1}. \qquad(1)\] Here, it is assumed that the prior probability is \({P}({{\mathcal{H}}_1}) = 0.5\), i.e., \({P}({{\mathcal{H}}_1}) = 1 - {P}({{\mathcal{H}}_1}) = {P}({{\mathcal{H}}_0})\). In [1], [2], a fixed SNR \({\xi_{{{\mathcal{H}}_1}}}\) is used which is interpreted as the local SNR that is expected if the hypothesis \({{\mathcal{H}}_1}\) holds. The likelihood models \({f}({{Y}_{{{k}, {\ell}}}}| {{\mathcal{H}}_0})\) and \({f}({{Y}_{{{k}, {\ell}}}}| {{\mathcal{H}}_1})\) have been used to formulate a speech detection problem in [2]. By minimizing the total probability of error [2], the optimal value \({\xi_{{{\mathcal{H}}_1}}}= -15~\text{dB}\) has been found.

In [1], [2], the posterior probability \({P}({{\mathcal{H}}_1}|{{Y}_{{{k}, {\ell}}}})\) is used to estimate the noise periodogram as \[ |{\hat{{N}}_{{{k}, {\ell}}}}|^2 = {P}({{\mathcal{H}}_0}|{{Y}_{{{k}, {\ell}}}}) |{{Y}_{{{k}, {\ell}}}}|^2 + {P}({{\mathcal{H}}_1}| {{Y}_{{{k}, {\ell}}}}) {\hat{\Lambda}^{n}_{{k}, {\ell}- 1}}. \qquad(2)\] Here, \({P}({{\mathcal{H}}_0}| {{Y}_{{{k}, {\ell}}}}) = 1 - {P}({{\mathcal{H}}_1}| {{Y}_{{{k}, {\ell}}}})\) is the speech absence probability. The estimated noise periodogram is smoothed over time to obtain the noise PSD estimate \({\hat{{N}}_{{{k}, {\ell}}}}\) as \[ {\hat{\Lambda}^{n}_{{{k}, {\ell}}}}= (1 - {\alpha}) |{{Y}_{{{k}, {\ell}}}}|^2 + {\alpha}{\hat{\Lambda}^{n}_{{k}, {\ell}- 1}}. \qquad(3)\] Here, \({\alpha}\) is a fixed smoothing constant. This estimator can be implemented in speech enhancement framework by evaluating equations 1, 2, and 3 for each new observation \({{Y}_{{{k}, {\ell}}}}\). A problem may arise if the noise PSD happens to be strongly underestimated. Then, the SPP in Equation 1 is overestimated, i.e., it is close to 1 and, as a result, the noise periodogram in Equation 2 may no longer be updated. To avoid such stagnations, the SPP is set to a lower value if it has been stuck at 1 for a longer period of time [1], [2].

Conventional Speech PSD Estimation [3], [4]

In [3], [4], a novel speech PSD estimator has been proposed which causes less musical tones in comparison to the well-known decision-directed approach. This approach is based on the maximum-likelihood estimator of the clean speech PSD \[ {\hat{\Lambda}^{{s}, \text{ml}}_{{{k}, {\ell}}}}= \max(|{{Y}_{{{k}, {\ell}}}}|^2 - {\hat{\Lambda}^{n}_{{{k}, {\ell}}}}, 0). \] The maximum-likelihood estimate of the clean speech PSD is transformed to the cepstral domain via \[ {\hat{\Lambda}^{{s}, \text{ml}}_{{q}, {\ell}}}= \text{IDFT}\{\log({\hat{\Lambda}^{{s}, \text{ml}}_{{{k}, {\ell}}}})\}, \] where \({q}\) is the quefrency index and \(\text{IDFT}(\cdot)\) denotes the inverse discrete Fourier transform. In the cepstral domain, speech can be represented by using only a few coefficients: The speech spectral envelope, which reflects the impact of the vocal tract filter, is represented by the lower coefficients with \({q}< 2.5 \text{ms}\) whereas the speech spectral fine structure, i.e., the fundamental frequency and its harmonics, is approximated by a single peak among the high cepstral coefficients. This peak is also referred to as pitch peak. The compact representation of speech is exploited by the temporal cepstrum smoothing approach by using a quefrency and time dependent smoothing constant \({\alpha_{{q}, {\ell}}}\) to smooth \({\hat{\Lambda}^{{s}, \text{ml}}_{{q}, {\ell}}}\) as \[ {\hat{\Lambda}^{s}_{{q}, {\ell}}}= (1 - {\alpha_{{q}, {\ell}}}) {\hat{\Lambda}^{{s}, \text{ml}}_{{q}, {\ell}}}+ {\alpha_{{q}, {\ell}}}{\hat{\Lambda}^{s}_{{q}, {\ell}- 1}}. \] For the cepstral coefficients that are associated with speech, only little smoothing is applied while the remaining cepstral coefficients are strongly smoothed. Accordingly, \({\alpha_{{q}, {\ell}}}\) is set close to 0 for the lower cepstral coefficients and close to 1 for the high coefficients.

The cepstrally smoothed speech PSD \({\hat{\Lambda}^{s}_{{q}, {\ell}}}\) is transformed back to the spectral domain as \[ {\hat{\Lambda}^{s}_{{{k}, {\ell}}}}= \exp(\text{DFT}\{{\hat{\Lambda}^{s}_{{q}, {\ell}}}\} + {\kappa}). \] As the smoothing in the cepstral domain results in a biased estimate [4], the correction term \({\kappa}\) is added. In [3], it has been argued that the bias of computing the expected value of a spectral quantity following a Gaussian distribution in the logarithmic domain amounts to the Euler constant. Due to the smoothing, the estimate in the cepstral domain is between an instantaneous value and the expected value. Hence, in [3], \({\kappa}\) is proposed to be set to \(1 / 2\) of the Euler constant, i.e., \({\kappa}\approx 0.5 \cdot 0.5772\dots\) is used. A more rigorous analysis of the bias and a more sophisticated algorithm for its compensation is given in [4].

Clean Speech Estimators [5]–[9]

The simplest Gain function is the Wiener gain \[ {{G}_{{{k}, {\ell}}}}= \frac{{\Lambda^{s}_{{{k}, {\ell}}}}}{{\Lambda^{s}_{{{k}, {\ell}}}}+ {\Lambda^{n}_{{{k}, {\ell}}}}} \] which is the MMSE optimal estimate of complex speech coefficients assuming that speech and noise follow a circular complex Gaussian distribution. More sophisticated estimators arise when estimates of functions of the clean speech coefficients are estimated or different assumptions on the underlying distributions are made. For instance, it has been argued that estimating compressed spectral amplitudes may be perceptually more meaningful than estimating complex speech coefficients. Furthermore, it has been shown that speech signals rather follow heavy-tailed super-Gaussian distributions rather than a Gaussian. Further, a wide range of phase-aware signal processing techniques have been presented in [5]–[9]. These range from methods to estimate clean speech phase [5], [6] to phase-aware clean speech estimators [7]–[9]. Further information about this topic can be found here.

References

[1] T. Gerkmann and R. C. Hendriks, “Noise Power Estimation Based on the Probability of Speech Presence,” in IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), 2011, pp. 145–148.

[2] T. Gerkmann and R. C. Hendriks, “Unbiased MMSE-Based Noise Power Estimation With Low Complexity and Low Tracking Delay,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 20, no. 4, pp. 1383–1393, May 2012.

[3] C. Breithaupt, T. Gerkmann, and R. Martin, “A novel a priori SNR estimation approach based on selective cepstro-temporal smoothing,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2008, pp. 4897–4900.

[4] T. Gerkmann and R. Martin, “On the Statistics of Spectral Amplitudes After Variance Reduction by Temporal Cepstrum Smoothing and Cepstral Nulling,” IEEE Transactions on Signal Processing, vol. 57, no. 11, pp. 4165–4174, 2009.

[5] M. Krawczyk and T. Gerkmann, “STFT Phase Improvement for Single Channel Speech Enhancement,” in International Workshop on Acoustic Signal Enhancement (IWAENC), 2012.

[6] M. Krawczyk and T. Gerkmann, “STFT Phase Reconstruction in Voiced Speech for an Improved Single-Channel Speech Enhancement,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 22, no. 12, pp. 1931–1940, Dec. 2014.

[7] T. Gerkmann, “Bayesian Estimation of Clean Speech Spectral Coefficients Given a Priori Knowledge of the Phase,” IEEE Transactions on Signal Processing, vol. 62, no. 16, pp. 4199–4208, Aug. 2014.

[8] T. Gerkmann, M. Krawczyk-Becker, and J. Le Roux, “Phase Processing for Single-Channel Speech Enhancement: History and recent advances,” IEEE Signal Processing Magazine, vol. 32, no. 2, pp. 55–66, Mar. 2015.

[9] M. Krawczyk-Becker and T. Gerkmann, “On MMSE-Based Estimation of Amplitude and Complex Speech Spectral Coefficients Under Phase-Uncertainty,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 24, no. 12, pp. 2251–2262, Dec. 2016.

[10] R. Rehr and T. Gerkmann, “On the Importance of Super-Gaussian Speech Priors for Machine-Learning Based Speech Enhancement,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 26, no. 2, pp. 357–366, Feb. 2018.

[11] G. Carbajal, J. Richter, T. Gerkmann,"Disentanglement Learning for Variational Autoencoders Applied to Audio-Visual Speech Enhancement", IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, Oct. 2021.

[12] J. Richter, G. Carbajal, T. Gerkmann, "Speech Enhancement with Stochastic Temporal Convolutional Networks", ISCA Interspeech, Shanghai, China, Oct. 2020.

[13] K. Tesch, T. Gerkmann, "Nonlinear Spatial Filtering in Multichannel Speech Enhancement", IEEE/ACM Trans. Audio, Speech, Language Proc., Vol. 29, pp. 1795-1805, 2021.